Despite the ongoing tragic events, we continue the series. In the last article we reviewed the stages of query execution. Before we move on to plan node operations (data access and join methods), let's discuss the bread and butter of the cost optimizer: statistics.

As usual, I use the demo database for all my examples. You can download it and follow along.

You will see a lot of execution plans here today. We will discuss how the plans work in more detail in later articles. For now just pay attention to the numbers that you see in the first line of each plan, next to the word rows. These are row number estimates, or cardinality.

Basic statistics

Basic relation-level statistics are stored in the table pg_class in the system catalog. The statistics include the following data:

• Relation's row count (reltuples).
• Relation's size in pages (relpages).
• Number of pages marked in the relation's visibility map (relallvisible).

SELECT reltuples, relpages, relallvisible
FROM pg_class WHERE relname = 'flights';

 reltuples | relpages | relallvisible
−−−−−−−−−−−+−−−−−−−−−−+−−−−−−−−−−−−−−−
    214867 |     2624 |         2624
(1 row)

For queries with no conditions (filters), the cardinality estimate will equal reltuples:

EXPLAIN SELECT * FROM flights;

                           QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on flights  (cost=0.00..4772.67 rows=214867 width=63)
(1 row)

Statistics are collected during automatic or manual analysis. Basic statistics, being vital information, are also calculated when some operations are performed, such as VACUUM FULL and CLUSTER or CREATE INDEX and REINDEX. The system also updates statistics during vacuuming.

To collect statistics, the analyzer randomly selects 300 × default_statistics_target rows (the default value is 100, so 30,000 rows in total). Table sizes are not taken into account here because overall dataset size has little effect on what sample size would be considered sufficient for accurate statistics.

Random rows are selected from 300 × default_statistics_target random pages. If a table is smaller than the desired sample size, the analyzer just reads the whole table.

In large tables, statistics will be imprecise because the analyzer does not scan every single row. Even if it did, the statistics would always be somewhat outdated, because table data keeps changing. We don't need the statistics to be all that precise anyway: variations up to an order of magnitude are still accurate enough to produce an adequate plan.

Let's create a copy of the flights table with autovacuuming disabled, so we can control when analysis happens.

CREATE TABLE flights_copy(LIKE flights)
WITH (autovacuum_enabled = false);

There are no statistics for the new table yet:

SELECT reltuples, relpages, relallvisible
FROM pg_class WHERE relname = 'flights_copy';

 reltuples | relpages | relallvisible
−−−−−−−−−−−+−−−−−−−−−−+−−−−−−−−−−−−−−−
        −1 |        0 |             0
(1 row)

The value reltuples = −1 (in PostgreSQL 14 and higher) helps us distinguish between a table that has never had statistics collected for it and a table that just doesn't have any rows.

More often than not, a newly created table is populated right away. The planner does not know anything about the new table, so it assumes the table to be 10 pages long by default:

EXPLAIN SELECT * FROM flights_copy;

                           QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on flights_copy  (cost=0.00..14.10 rows=410 width=170)
(1 row)

The planner calculates the row count based on the width of a single row. The width is usually an average value that's calculated during analysis. This time, however, there is no analysis data, so the system approximates the width based on column data types.

Let's copy the data from flights into the new table and run the analyzer:

INSERT INTO flights_copy SELECT * FROM flights;

INSERT 0 214867

ANALYZE flights_copy;

Now the statistics match the actual row count. The table is compact enough for the analyzer to run through every row:

SELECT reltuples, relpages, relallvisible
FROM pg_class WHERE relname = 'flights_copy';

 reltuples | relpages | relallvisible
−−−−−−−−−−−+−−−−−−−−−−+−−−−−−−−−−−−−−−
    214867 |     2624 |             0
(1 row)

The relallvisible value updates after vacuuming:

VACUUM flights_copy;
SELECT relallvisible FROM pg_class WHERE relname = 'flights_copy';

 relallvisible
−−−−−−−−−−−−−−−
          2624
(1 row)

This value is used when estimating index-only scan cost.

Let's double the number of rows while keeping the old statistics and see what cardinality the planner comes up with:

INSERT INTO flights_copy SELECT * FROM flights;
SELECT count(*) FROM flights_copy;

 count
−−−−−−−−
 429734
(1 row)

EXPLAIN SELECT * FROM flights_copy;

                            QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on flights_copy  (cost=0.00..9545.34 rows=429734 width=63)
(1 row)

The estimate is accurate, despite the outdated pg_class data:

SELECT reltuples, relpages
FROM pg_class WHERE relname = 'flights_copy';

 reltuples | relpages
−−−−−−−−−−−+−−−−−−−−−−
    214867 |     2624
(1 row)

The planner notices that the size of the data file no longer matches the old relpages value, so it scales reltuples appropriately in an attempt to increase accuracy. The file size has doubled, so the number of rows is adjusted accordingly (data density is presumed constant):

SELECT reltuples *
  (pg_relation_size('flights_copy') / 8192) / relpages
FROM pg_class WHERE relname = 'flights_copy';

 ?column?
−−−−−−−−−−
   429734
(1 row)

This adjustment doesn't always work (for example, you can delete several rows, and the estimate will not change), but when big changes are made, this approach allows the statistics to hold on until the analyzer comes around.

NULL values

While looked down upon by purists, NULL values serve as a convenient representation of values that are unknown or nonexistent.

But special values require special treatment. There are practical considerations to keep in mind when working with NULL values. Boolean logic turns into ternary, and the NOT IN construction starts behaving weirdly. It's unclear whether NULL values are to be considered lower or higher than conventional values (special clauses NULLS FIRST and NULLS LAST help out with that). The use of NULL values in aggregate functions is sketchy, too. Because NULL values are, in fact, not values at all, the planner needs extra data to accommodate them.

In addition to basic relation-level statistics, the analyzer also collects statistics for each column in a relation. This data is stored in the pg_statistic table in the system catalog and can be conveniently displayed using the pg_stats view.

Fraction of null values is column-level statistics. It's designated as null_frac in pg_stats. In this example some planes haven't departed yet, so their time of departure is undefined:

EXPLAIN SELECT * FROM flights WHERE actual_departure IS NULL;

                          QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on flights  (cost=0.00..4772.67 rows=16036 width=63)
   Filter: (actual_departure IS NULL)
(2 rows)

The optimizer multiplies the total row count by the NULL fraction:

SELECT round(reltuples * s.null_frac) AS rows
FROM pg_class
  JOIN pg_stats s ON s.tablename = relname
WHERE s.tablename = 'flights'
  AND s.attname = 'actual_departure';

 rows
−−−−−−−
 16036
(1 row)

This is close enough to the true value of 16348.

Distinct values

The number of distinct values in a column is stored in the n_distinct field in pg_stats.

If n_distinct is negative, its absolute value instead represents the fraction of values that are distinct. For example, the value of −1 means that every item in the column is unique. When the number of distinct values reaches 10% of the number of rows or more, the analyzer switches to the fraction mode. It is assumed at this point that the proportion will generally remain the same when the data is modified.

If the number of distinct values is calculated incorrectly (because the sample happened to be unrepresentative), you can set this value manually:

ALTER TABLE ... ALTER COLUMN ... SET (n_distinct = ...);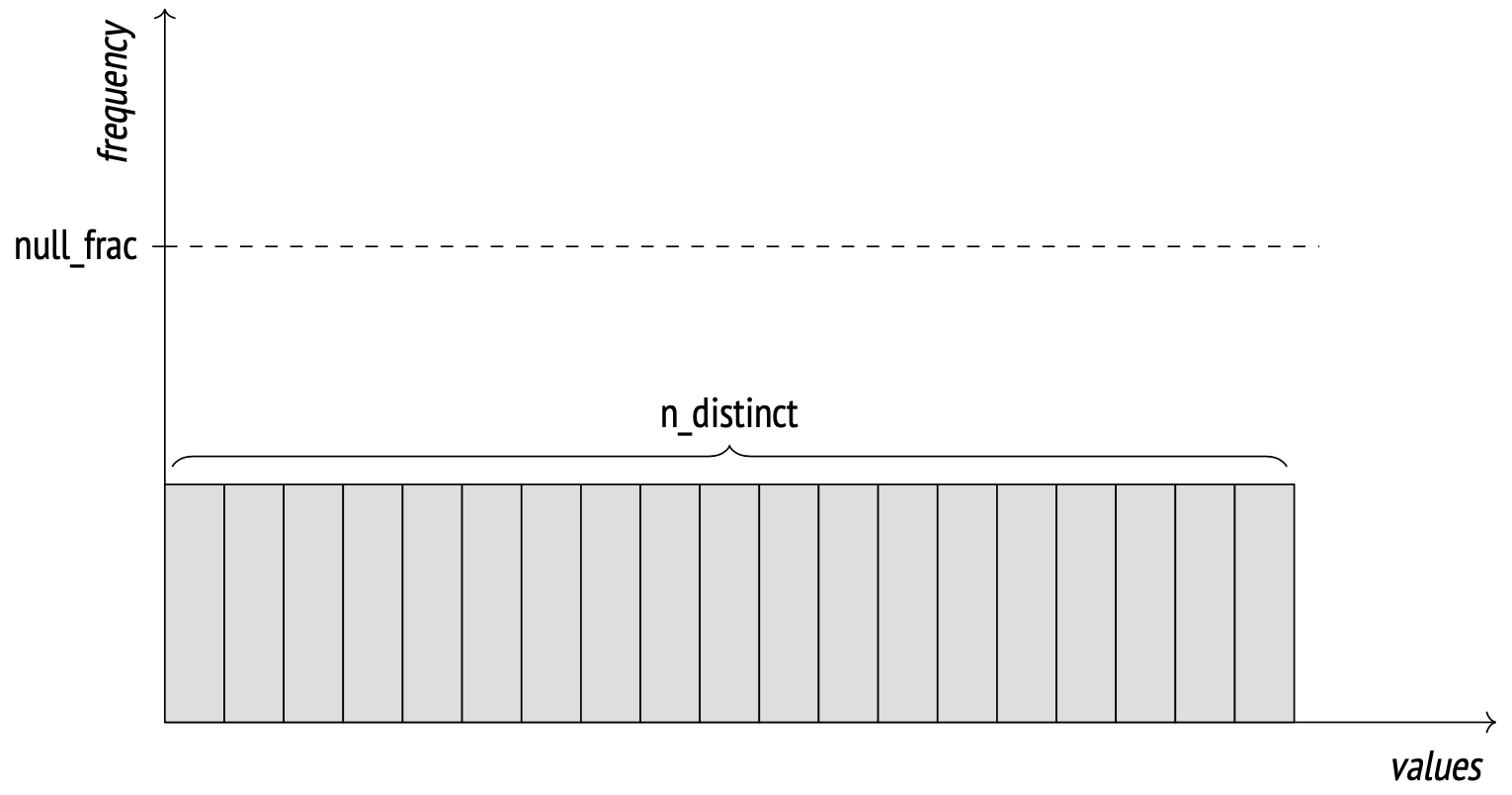

The number of distinct values is useful in cases where data is distributed uniformly. Consider this cardinality estimation of a "column = expression" clause. If the value of expression is unknown at the planning stage, the planner assumes that expression is equally likely to return any value from the column.

EXPLAIN
SELECT * FROM flights WHERE departure_airport = (
  SELECT airport_code FROM airports WHERE city = 'Saint Petersburg'
);

                         QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on flights  (cost=30.56..5340.40 rows=2066 width=63)
   Filter: (departure_airport = $0)
   InitPlan 1 (returns $0)
     −> Seq Scan on airports_data ml  (cost=0.00..30.56 rows=1 wi...
         Filter: ((city −>> lang()) = 'Saint Petersburg'::text)
(5 rows)

The InitPlan node is executed only once, and the value is then used instead of $0 in the main plan.

SELECT round(reltuples / s.n_distinct) AS rows
FROM pg_class
  JOIN pg_stats s ON s.tablename = relname
WHERE s.tablename = 'flights'
  AND s.attname = 'departure_airport';

 rows
−−−−−−
 2066
(1 row)

If all data is distributed uniformly, these statistics (together with min and max values) would be sufficient for an accurate estimation. Unfortunately, this estimation does not work as well for nonuniform distributions, which are much more common:

SELECT min(cnt), round(avg(cnt)) avg, max(cnt) FROM (
  SELECT departure_airport, count(*) cnt
  FROM flights GROUP BY departure_airport
) t;

 min | avg  |  max
−−−−−+−−−−−−+−−−−−−−
 113 | 2066 | 20875
(1 row)

Most common values

To improve estimation accuracy for non-uniform distributions, the analyzer collects statistics on most common values (MCVs) and their frequency. These values are stored in pg_stats as most_common_vals and most_common_freqs.

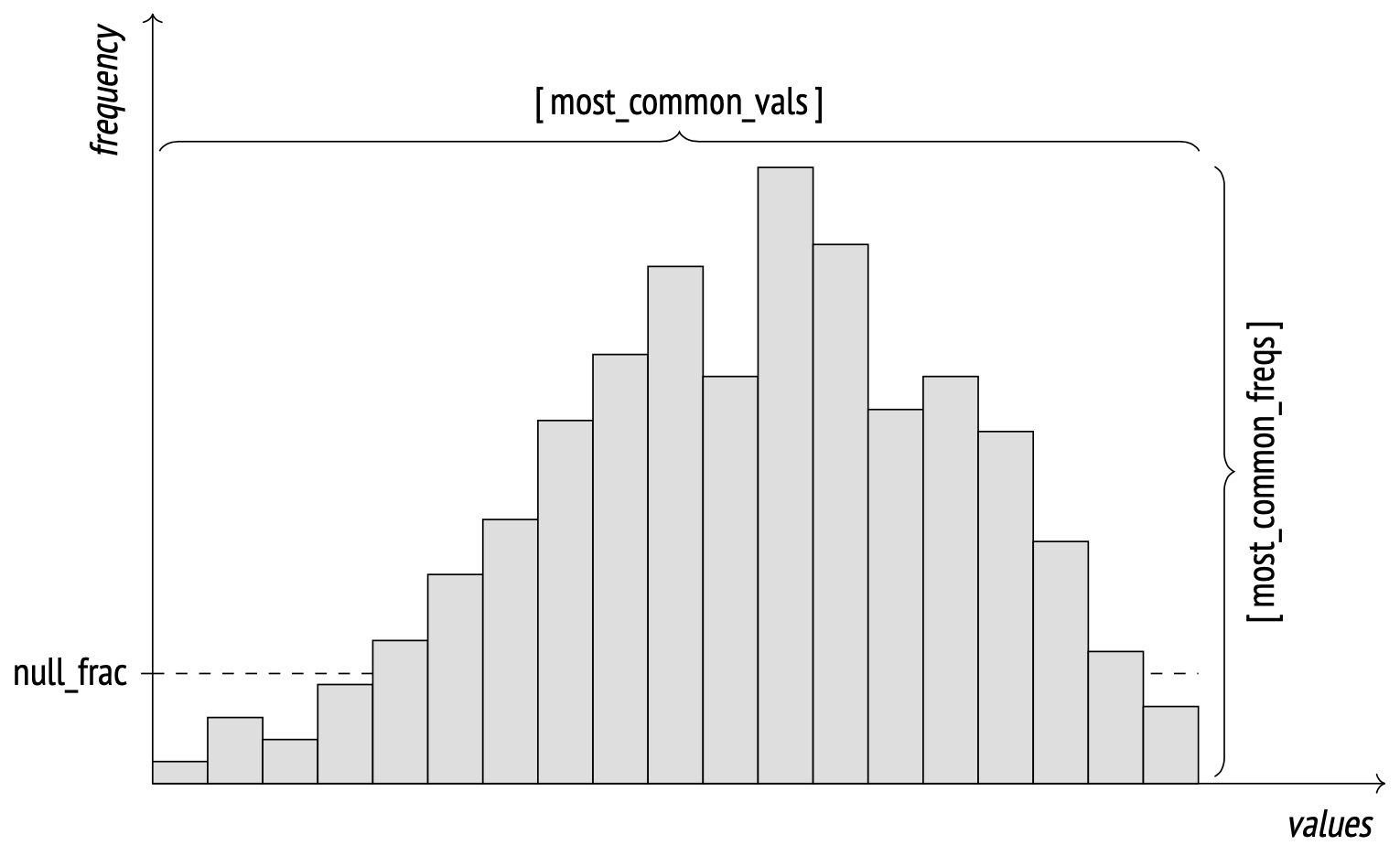
Here's an example of such statistics for the most common aircraft types:

SELECT most_common_vals AS mcv,
  left(most_common_freqs::text,60) || '...' AS mcf
FROM pg_stats
WHERE tablename = 'flights' AND attname = 'aircraft_code' \gx

 −[ RECORD 1 ]−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
mcv | {CN1,CR2,SU9,321,763,733,319,773}
mcf | {0.2783,0.27473333,0.25816667,0.059233334,0.038533334,0.0370...

Estimating selectivity of "column = expression" is extremely straightforward: the planner just takes a value from the most_common_vals array and multiplies it by the frequency from the same position in the most_common_freqs array.

EXPLAIN SELECT * FROM flights WHERE aircraft_code = '733';

                          QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on flights  (cost=0.00..5309.84 rows=7957 width=63)
   Filter: (aircraft_code = '733'::bpchar)
(2 rows)

SELECT round(reltuples * s.most_common_freqs[
  array_position((s.most_common_vals::text::text[]),'733')
])
FROM pg_class
  JOIN pg_stats s ON s.tablename = relname
WHERE s.tablename = 'flights'
  AND s.attname = 'aircraft_code';

 round
−−−−−−−
  7957
(1 row)

This estimate will be close to the true value of 8263.

MCV lists are also used for selectivity estimations of inequalities: to find the selectivity of "column < value", the planner searches most_common_vals for all the values lower than the given value, and then adds together their frequencies from most_common_freqs.

Common value statistics work best when the number of distinct values is low. The maximum size of the MCV arrays is defined by default_statistics_target, the same parameter that governs row sample size during analysis.

In some cases increasing the value (and thus the array size) beyond the default value will provide more accurate estimations. You can set this value per column:

ALTER TABLE ... ALTER COLUMN ... SET STATISTICS ...;

The row sample size will increase as well, but only for the table.

The common values array stores the values themselves and, depending on the values, could take up a lot of space. This is why values over 1 kB in size are excluded from analysis and statistics. It keeps pg_statistic size under control and does not overload the planner. Values this large are usually distinct anyway and wouldn't get included in most_common_vals.

Histogram

When the number of distinct values grows too large to store them all in an array, the system starts using the histogram representation. A histogram employs several buckets to store values in. The number of buckets is limited by the same default_statistics_target parameter.

The width of each bucket is selected in such a way as to distribute the values evenly across them (as indicated by the rectangles on the image having approximately the same area). This representation enables the system to store only histogram bounds, not wasting space for storing the frequency of each bucket. Histograms do not include values from MCV lists.

The bounds are stored in the histogram_bounds field in pg_stats. The summary frequency of values in any bucket equals 1 / number of buckets.

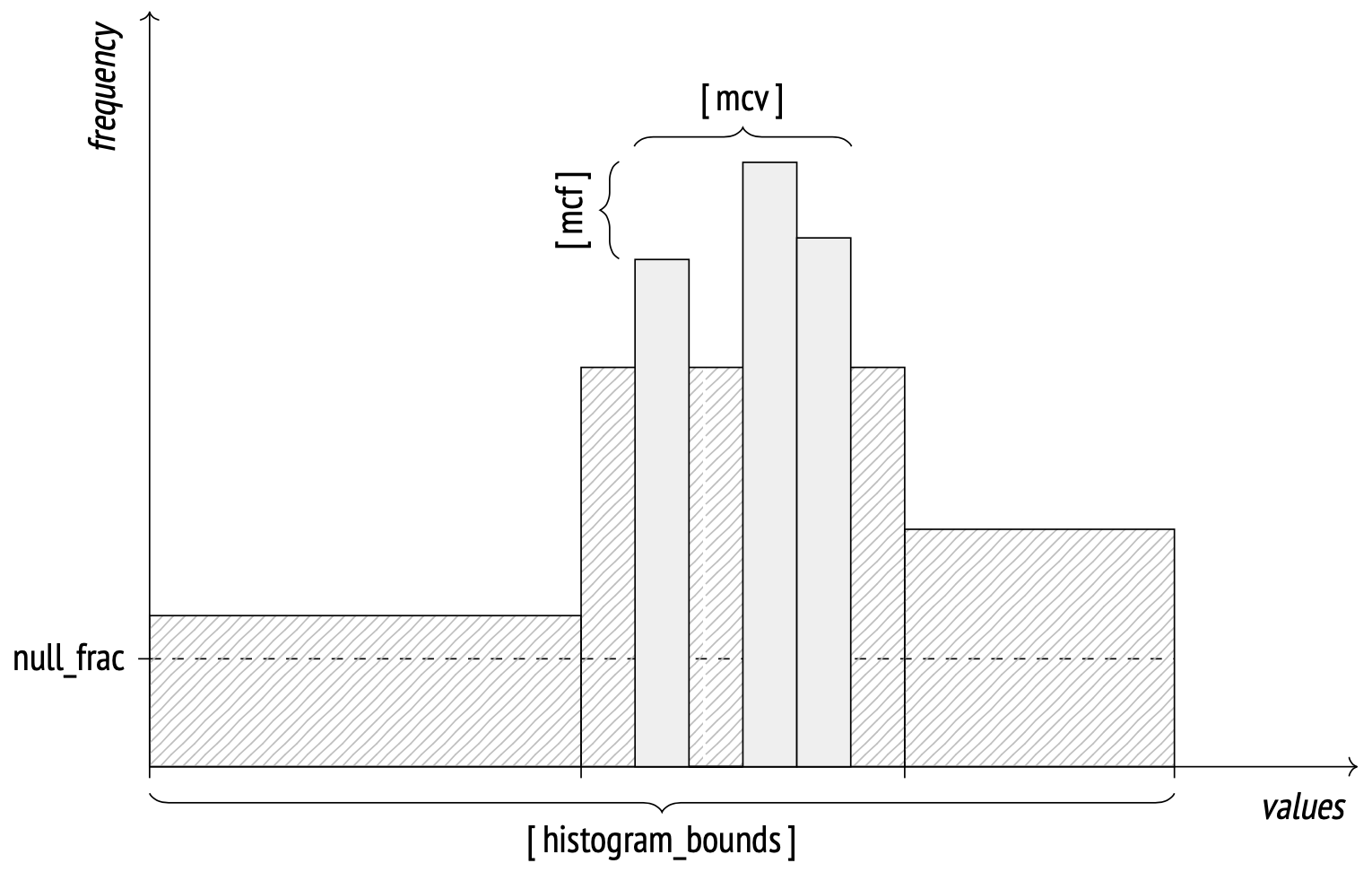
A histogram is stored as an array of bucket bounds:

SELECT left(histogram_bounds::text,60) || '...' AS histogram_bounds
FROM pg_stats s
WHERE s.tablename = 'boarding_passes' AND s.attname = 'seat_no';

                        histogram_bounds
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 {10B,10D,10D,10F,11B,11C,11H,12H,13B,14B,14H,15H,16D,16D,16H...
(1 row)

Among other things, histograms are used to estimate selectivity of "greater than" and "less than" operations together with MCV lists.

Example: calculating the number of boarding passes issued for seats in the back.

EXPLAIN SELECT * FROM boarding_passes WHERE seat_no > '30C';

                             QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on boarding_passes  (cost=0.00..157353.30 rows=2943394 ...
   Filter: ((seat_no)::text > '30C'::text)
(2 rows)

The cutoff seat number is selected specifically to be on the edge between two buckets.

The selectivity of this condition is N / number of buckets, where N is the number of buckets with matching values (to the right of the cutoff point). Remember that histograms don't take into account most common values and undefined values.

Let's look at the fraction of matching most common values first:

SELECT sum(s.most_common_freqs[
  array_position((s.most_common_vals::text::text[]),v)
])
FROM pg_stats s, unnest(s.most_common_vals::text::text[]) v
WHERE s.tablename = 'boarding_passes' AND s.attname = 'seat_no'
AND v > '30C';

  sum
−−−−−−−−
 0.2127
(1 row)

Now let's look at the fraction of most common values (excluded from the histogram):

SELECT sum(s.most_common_freqs[
  array_position((s.most_common_vals::text::text[]),v)
])
FROM pg_stats s, unnest(s.most_common_vals::text::text[]) v
WHERE s.tablename = 'boarding_passes' AND s.attname = 'seat_no';

  sum
−−−−−−−−
 0.6762
(1 row)

There are no NULL values in the seat_no column:

SELECT s.null_frac
FROM pg_stats s
WHERE s.tablename = 'boarding_passes' AND s.attname = 'seat_no';

 null_frac
−−−−−−−−−−−
         0
(1 row)

The interval covers exactly 49 buckets (out of 100 total). The resulting estimate:

SELECT round( reltuples * (
   0.2127 -- from most common values
 + (1 - 0.6762 - 0) * (49 / 100.0) -- from histogram
))
FROM pg_class WHERE relname = 'boarding_passes';

  round
−−−−−−−−−
 2943394
(1 row)

The true value is 2986429.

When the cutoff value isn't at the edge of a bucket, the matching fraction of that bucket is calculated using linear interpolation.

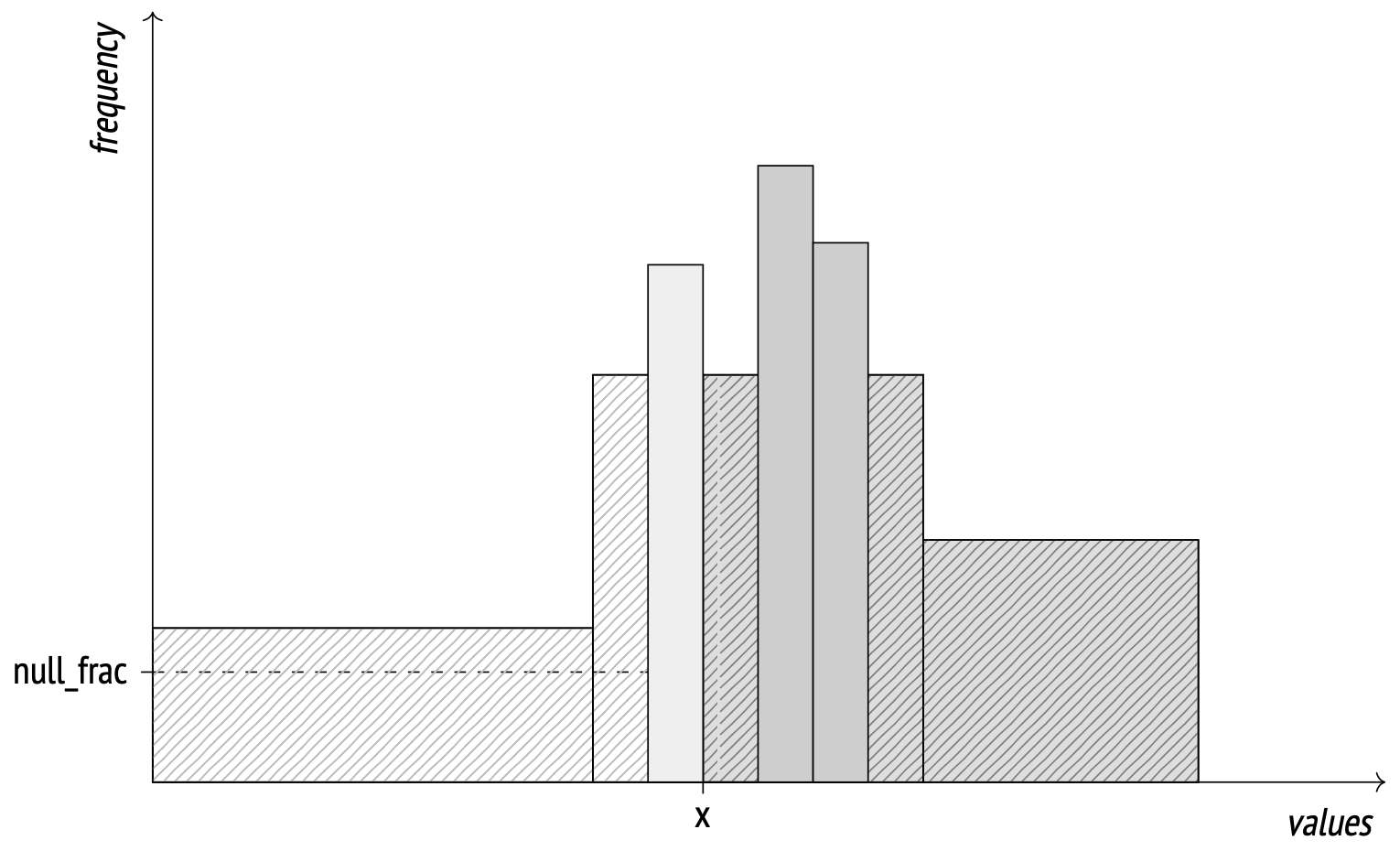
Higher default_statistics_target value may improve estimate accuracy, but the histogram together with the MCV list already produce a good result, even with a high number of distinct values:

SELECT n_distinct FROM pg_stats
WHERE tablename = 'boarding_passes' AND attname = 'seat_no';

 n_distinct
−−−−−−−−−−−−
        461
(1 row)

Higher estimate accuracy is beneficial only as long as it improves planning quality. Increasing default_statistics_target without a valid reason may slow analysis and planning while having no effect on optimization.

On the other hand, lowering the parameter (all the way down to zero) may increase analysis and planning speed, but may also result in low-quality plans, so this "time save" is rarely justified.

Statistics for nonscalar data types

Statistics for nonscalar data types may include distribution data not only for the nonscalar values themselves, but for their comprising elements as well. This allows for more accurate planning when columns in forms other than the first normal form are queried.

• The arrays most_common_elems and most_common_elem_freqs contain most common elements and their frequencies, respectively.

  These statistics are collected and used to estimate selectivity of arrays and tsvector data.

• elem_count_histogram array is a histogram of the number of distinct elements in a value.

  These statistics are collected and used to estimate selectivity of arrays only.

• For range data types, histograms are used to represent the distribution of range length and distributions of its lower and upper bounds. These histograms then help estimate selectivity for various operations with these data types. They are not shown in pg_stats.

  These statistics are also used for multirange data types introduced in PostgreSQL 14.

Average field width

The avg_width field in pg_stats represents the average filed width in a column. Field width for data types such as integer or char(3) is obviously fixed, but when it comes to data types with no set width, such as text, the value may differ significantly column to column:

SELECT attname, avg_width FROM pg_stats
WHERE (tablename, attname) IN ( VALUES
  ('tickets', 'passenger_name'), ('ticket_flights','fare_conditions')
);

     attname     | avg_width
−−−−−−−−−−−−−−−−−+−−−−−−−−−−−
 fare_conditions |         8
 passenger_name  |        16
(2 rows)

These statistics help estimate memory usage for operations like sorting or hashing.

Correlation

The field correlation in pg_stats represents correlation between physical row ordering on disk and logical ordering ("greater than" or "less than") of the column values, ranging from -1 to +1. If the values are stored in order, correlation will be close to +1. If they are stored in reverse order, then correlation will be closer to -1. The more chaotically the data is distributed on the disk, the closer the value will be to zero.

SELECT attname, correlation
FROM pg_stats WHERE tablename = 'airports_data'
ORDER BY abs(correlation) DESC;

   attname    | correlation
−−−−−−−−−−−−−−+−−−−−−−−−−−−−
 coordinates  |
 airport_code | −0.21120238
 city         |  −0.1970127
 airport_name | −0.18223621
 timezone     |  0.17961165
(5 rows)

The statistics for the coordinates column can't be collected, because comparison operations ("less than" and "greater than") are not defined for the point data type.

Correlation is used for index scan cost estimation.

Expression statistics

Generally speaking, column statistics are only used when an operation calls for the column itself, not for an expression with the column as a parameter. The planner doesn't know how a function will affect column statistics, so conditions like "function-call = constant" are always estimated at 0.5%:

EXPLAIN SELECT * FROM flights
WHERE extract(
  month FROM scheduled_departure AT TIME ZONE 'Europe/Moscow'
) = 1;

                             QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on flights  (cost=0.00..6384.17 rows=1074 width=63)
   Filter: (EXTRACT(month FROM (scheduled_departure AT TIME ZONE ...
(2 rows)

SELECT round(reltuples * 0.005)
FROM pg_class WHERE relname = 'flights';

 round
−−−−−−−
  1074
(1 row)

The planner can't process even standard functions, while to us it's obvious that the fraction of flights in January will be around 1/12 of total flights:

SELECT count(*) AS total,
  count(*) FILTER (WHERE extract(
    month FROM scheduled_departure AT TIME ZONE 'Europe/Moscow'
  ) = 1) AS january
FROM flights;

 total  | january
−−−−−−−−+−−−−−−−−−
 214867 |   16831
(1 row)

This is where expression statistics come in.

Extended expression statistics

PostgreSQL 14 introduced a feature known as extended expression statistics. Extended expression statistics aren't collected automatically. To collect them manually, use the CREATE STATISTICS command to create an extended statistics database object.

CREATE STATISTICS flights_expr ON (extract(
  month FROM scheduled_departure AT TIME ZONE 'Europe/Moscow'
))
FROM flights;

The new statistics will improve the estimate:

ANALYZE flights;
EXPLAIN SELECT * FROM flights
WHERE extract(
  month FROM scheduled_departure AT TIME ZONE 'Europe/Moscow'
) = 1;

                             QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on flights  (cost=0.00..6384.17 rows=16222 width=63)
   Filter: (EXTRACT(month FROM (scheduled_departure AT TIME ZONE ...
(2 rows)

For the statistics to work, the expression in the statistics generation command must be identical to the one in the original query.

Extended statistics metadata is stored in the pg_statistic_ext table in the system catalog, while the statistics data itself is stored in a separate table pg_statistic_ext_data (in PostgreSQL 12 and higher). It is stored separately from the metadata to restrict user access to sensitive information, if necessary.

There are views that display collected statistics in a user-friendly form. Extended expression statistics can be displayed with the following command:

SELECT left(expr,50) || '...' AS expr,
  null_frac, avg_width, n_distinct,
  most_common_vals AS mcv,
  left(most_common_freqs::text,50) || '...' AS mcf,
  correlation
FROM pg_stats_ext_exprs WHERE statistics_name = 'flights_expr' \gx

-[ RECORD 1 ]−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
expr        | EXTRACT(month FROM (scheduled_departure AT TIME ZO...
null_frac   | 0
avg_width   | 8
n_distinct  | 12
mcv         | {8,9,3,5,12,4,10,7,11,1,6,2}
mcf         | {0.12526667,0.11016667,0.07903333,0.07903333,0.078..
correlation | 0.095407926

The amount of collected statistics data can be altered with the ALTER STATISTICS command:

ALTER STATISTICS flights_expr SET STATISTICS 42;

Expression index statistics

When an expression index is built, the system collects its statistics, just like with a regular table. The planner can use these statistics too. It's convenient, but only if we actually care about the index.

DROP STATISTICS flights_expr;
CREATE INDEX ON flights(extract(
  month FROM scheduled_departure AT TIME ZONE 'Europe/Moscow'
)); => ANALYZE flights;
EXPLAIN SELECT * FROM flights WHERE extract(
  month FROM scheduled_departure AT TIME ZONE 'Europe/Moscow'
) = 1;

                             QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Bitmap Heap Scan on flights  (cost=318.42..3235.96 rows=16774 wi...
   Recheck Cond: (EXTRACT(month FROM (scheduled_departure AT TIME...
   −> Bitmap Index Scan on flights_extract_idx  (cost=0.00..314.2...
       Index Cond: (EXTRACT(month FROM (scheduled_departure AT TI...
(4 rows)

Expression index statistics are stored in the same way table statistics are. For example, this is the number of distinct values:

SELECT n_distinct FROM pg_stats
WHERE tablename = 'flights_extract_idx';

 n_distinct
−−−−−−−−−−−−
         12
(1 row)

In PostgreSQL 11 and higher, the accuracy of index statistics can be changed with the ALTER INDEX command. You might need the name of the column that references the expression. Example:

SELECT attname FROM pg_attribute
WHERE attrelid = 'flights_extract_idx'::regclass;

 attname
−−−−−−−−−
 extract
(1 row)

ALTER INDEX flights_extract_idx
  ALTER COLUMN extract SET STATISTICS 42;

Multivariate statistics

PostgreSQL 10 introduced the ability to collect statistics from several columns simultaneously, also known as multivariate statistics. This requires generating the necessary extended statistics manually.

There are three types of multivariate statistics.

Functional dependencies between columns

When values in one column are determined (fully or partially) by values in another column, and there are conditions referencing both columns in a query, the resulting cardinality will be underestimated.

Here's an example with two conditions:

SELECT count(*) FROM flights
WHERE flight_no = 'PG0007' AND departure_airport = 'VKO';

 count
−−−−−−−
   396
(1 row)

The estimate is significantly lower than it should be, at just 26 rows:

EXPLAIN SELECT * FROM flights
WHERE flight_no = 'PG0007' AND departure_airport = 'VKO';

                             QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Bitmap Heap Scan on flights  (cost=12.03..1238.70 rows=26 width=63)
   Recheck Cond: (flight_no = 'PG0007'::bpchar)
   Filter: (departure_airport = 'VKO'::bpchar)
   −> Bitmap Index Scan on flights_flight_no_scheduled_departure_key
       (cost=0.00..12.02 rows=480 width=0)
       Index Cond: (flight_no = 'PG0007'::bpchar)
(6 rows)

This is the infamous correlated predicates problem. The planner expects the predicates to be independent and calculates the resulting selectivity as the product of selectivities of the conditions, combined with AND. The Bitmap Index Scan estimate, calculated for the flight_no condition, drops significantly after the departure_airport condition in Bitmap Heap Scan is applied.

Naturally, a flight number already unambiguously defines the departure airport, so the second condition is actually redundant. This is where extended functional dependencies statistics can help improve the estimate.

Let's create extended functional dependencies statistics for the two columns:

CREATE STATISTICS flights_dep(dependencies)
ON flight_no, departure_airport FROM flights;

Analyze again, now with the new statistics, and the estimate improves:

ANALYZE flights;
EXPLAIN SELECT * FROM flights
WHERE flight_no = 'PG0007' AND departure_airport = 'VKO';

                             QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Bitmap Heap Scan on flights  (cost=10.56..816.91 rows=276 width=63)
   Recheck Cond: (flight_no = 'PG0007'::bpchar)
   Filter: (departure_airport = 'VKO'::bpchar)
   −> Bitmap Index Scan on flights_flight_no_scheduled_departure_key
       (cost=0.00..10.49 rows=276 width=0)
       Index Cond: (flight_no = 'PG0007'::bpchar)
(6 rows)

The statistics are stored in the system catalog and can be displayed with this command:

SELECT dependencies
FROM pg_stats_ext WHERE statistics_name = 'flights_dep';

               dependencies
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 {"2 => 5": 1.000000, "5 => 2": 0.010567}
(1 row)

The numbers 2 and 5 are the table column numbers from pg_attribute. The values next to them represent the degree of functional dependency, from 0 (independent) to 1 (values in the second column are entirely defined by values in the first one).

Multivariate number of distinct values

Statistics on the number of distinct combinations of values from several columns will significantly improve the cardinality of a GROUP BY operation over multiple columns.

In this example, the planner estimates the number of possible pairs of departure and arrival airports as the total number of airports squared. The true number of pairs is significantly lower, however, because not every two airports are connected by direct flights:

SELECT count(*) FROM (
  SELECT DISTINCT departure_airport, arrival_airport FROM flights
) t;

 count
−−−−−−−
   618
(1 row)

EXPLAIN
SELECT DISTINCT departure_airport, arrival_airport FROM flights;

                             QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 HashAggregate  (cost=5847.01..5955.16 rows=10816 width=8)
   Group Key: departure_airport, arrival_airport
   −> Seq Scan on flights  (cost=0.00..4772.67 rows=214867 width=8)
(3 rows)

Let's create an extended statistics for the number of distinct values:

CREATE STATISTICS flights_nd(ndistinct)
ON departure_airport, arrival_airport FROM flights;
ANALYZE flights;
EXPLAIN
SELECT DISTINCT departure_airport, arrival_airport FROM flights;

                             QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 HashAggregate (cost=5847.01..5853.19 rows=618 width=8)
   Group Key: departure_airport, arrival_airport
   −> Seq Scan on flights  (cost=0.00..4772.67 rows=214867 width=8)
(3 rows)

The statistics are stored in the system catalog:

SELECT n_distinct
FROM pg_stats_ext WHERE statistics_name = 'flights_nd';

  n_distinct
−−−−−−−−−−−−−−−
 {"5, 6": 618}
(1 row)

Multivariate most common values lists

When values are distributed non-uniformly, functional dependency data alone may not suffice, as the estimate will vary significantly depending on specific pairs of values. Consider this example, where the planner inaccurately estimates the number of flights from Sheremetyevo airport made by Boeing 737:

SELECT count(*) FROM flights
WHERE departure_airport = 'SVO' AND aircraft_code = '733'

 count
−−−−−−−
  2037
(1 row)

EXPLAIN SELECT * FROM flights
WHERE departure_airport = 'SVO' AND aircraft_code = '733';

                             QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on flights  (cost=0.00..5847.00 rows=733 width=63)
   Filter: ((departure_airport = 'SVO'::bpchar) AND (aircraft_cod...
(2 rows)

We can improve the estimate with multivariate MCV list statistics:

CREATE STATISTICS flights_mcv(mcv)
ON departure_airport, aircraft_code FROM flights;
ANALYZE flights;
EXPLAIN SELECT * FROM flights
WHERE departure_airport = 'SVO' AND aircraft_code = '733';

                             QUERY PLAN
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Seq Scan on flights  (cost=0.00..5847.00 rows=2077 width=63)
   Filter: ((departure_airport = 'SVO'::bpchar) AND (aircraft_cod...
(2 rows)

Now there is frequency data in the system catalog for the planner to use:

SELECT values, frequency
FROM pg_statistic_ext stx
  JOIN pg_statistic_ext_data stxd ON stx.oid = stxd.stxoid,
  pg_mcv_list_items(stxdmcv) m
WHERE stxname = 'flights_mcv'
AND values = '{SVO,773}';

  values   |      frequency
−−−−−−−−−−−+−−−−−−−−−−−−−−−−−−−−−−
 {SVO,773} | 0.005733333333333333
(1 row)

A multivariate most common values list stores default_statistics_target values, just like a regular MCV list. If the parameter is defined at the column level, the highest value is used.

As with extended expression statistics, you can change the list size (in PostgreSQL 13 and higher):

ALTER STATISTICS ... SET STATISTICS ...;

In these examples, multivariate statistics are collected for only two columns, but you can collect them for as many columns as you want.

You can also collect different types of statistics into a single extended statistics object. To do this, just list required statistics types separated by commas when creating an object. If no specific statistics types are defined, the system will collect all available statistics at once.

PostgreSQL 14 also allows you to use not just column names, but arbitrary expressions when making multivariate and expression statistics.

Read on.